Szerelmi háromszög és más matekpéldák

A „végtelen” felfoghatatlan, inkább metaforának tűnik, mint egzakt természettudományos fogalomnak.

A matematikai terminusra épülő költői metafora igencsak hálás holmi. Egyrészt, mert világosnak, relevánsnak érezzük tiszta fogalmi jelentése miatt. Másrészt a kontraszt, ami a lelki folyamatok kimondhatatlansága és a matematika egyértelműsége között van, mégis eredetivé, nagyobb poétikai erejűvé teszi a költői képet: „Megyünk és hallgatunk. Huszonhárom év van köztünk. A huszonhármat nem lehet osztani. A huszonhárom csak magával osztható. Meg eggyel. Ilyen magány van köztünk.” (Borbély Szilárd)

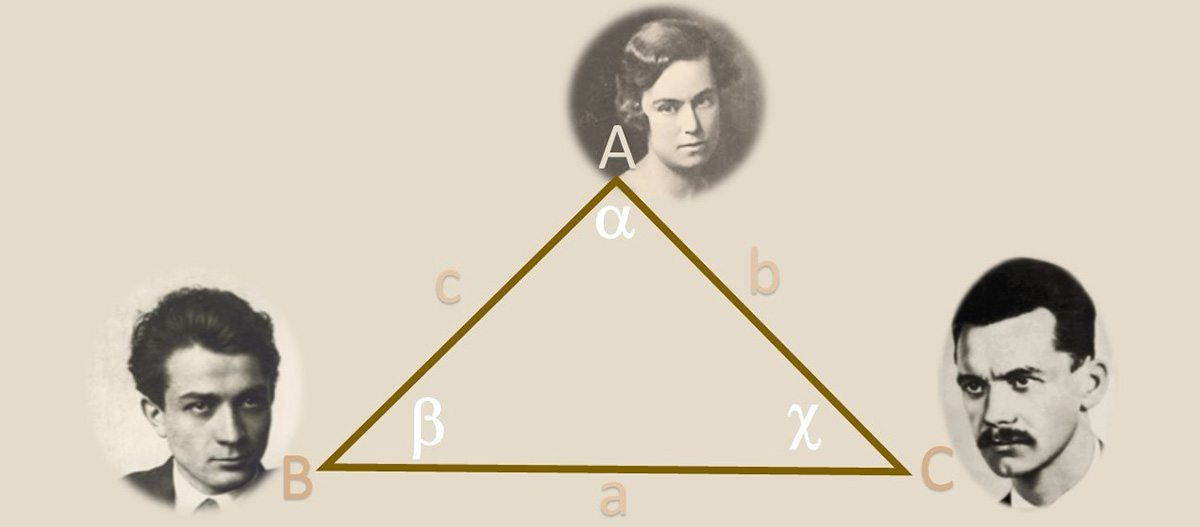
A matematikai terminusokból származtatott metaforának persze nem kell olyan egyértelműnek lennie, mint az egyszeregynek – (lásd még: kockás füzet, hasábburgonya, baráti kör), az ember nyelvészként mégis szívesen ered e kifejezések nyomába. Vegyük például az Illyés Gyula – József Attila – Vágó Márta viszonyrendszert (Vágó Márta természetesen behelyettesíthető Kozmutza Flórával is, tetszés szerint). Íme a klasszikus szerelmi háromszög:

De mi a hiba a fenti ábrán? A háromszögnek három csúcsa van (A, B és C, a három érintett személy), és a csúcsokat három vonal köti össze: a, b és c (ez jelentené a szerelmi viszonyt). Ám a szerelmi háromszög fogalma így értelemszerűen azt jelentené, hogy a három ember közül mindegyik szerelmes a másik kettőbe. Illyés és József Attila viszonya azért mégsem így írható le, tehát korrigálnunk kell az ábrát:

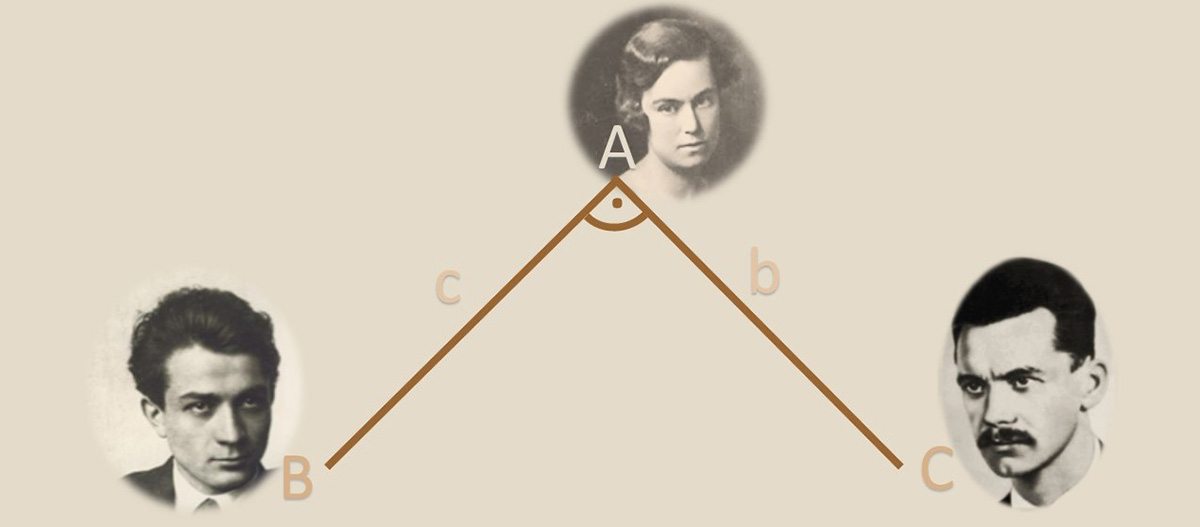
Csak a három pont maradt meg: a három személy, az összekötő három vonalból pedig csak kettő, a két „szeretés” (a befogók – mert Vágó Márta igazán megérdemli a derékszöget).  De hova tűnt a háromszög? Egyetlen szöggé zsugorodott. Nevezhetjük ezt „szerelmi szögnek” – de nem háromszögnek, hiszen hiányzik az átfogó.

Mégis, nehéz lenne frappánsabb kifejezést találni erre a szituációra. A költői kép valótlanság (sőt, a valósághoz képest hazugság), gyakran mégis többet mond a lényegről, mélyebben érinti a képzeletet és az érzékeket a szó szerint kifejezett gondolathoz képest.

A matematikai-logikai gondolkodás meghatározza mindennapi nyelvhasználatunkat, enélkül nem tudnánk a legegyszerűbb jelenségeket sem felfogni, sem megnevezni.

Bármikor, amikor nyelvi kategóriákban, definíciókban gondolkodunk, észre sem vesszük, hogy halmazműveletet végzünk.

Mi egyszerűbben, az írók-költők merészebben:

„Tekintsük A halmazt. Ez legyen a prímszámok halmaza. Egy pozitív egész számot prímszámnak nevezünk, ha 1-en és önmagán kívül más egész számmal nem osztható. (…) B halmaz legyen a valaha élt magyar írók halmaza (…). Írónak azt nevezzük… hát lényegében, amit prímnek, hogy az egyen és önmagán kívül ne legyen más osztója (lásd még: a mindenséggel mérd magad!), ha pedig valaki író és magyarul ír, az magyar író.” (Esterházy Péter)

A matematika, a nyelv – és ennél fogva az irodalom – összefüggése évszázadokon keresztül kézenfekvő volt, ám az idők során a humán-reál egymást kiegészítő fogalma inkább oppozícióvá vált a fejekben. Bölcsész körökben illő kérkedni a matematikai defektusokkal (mintha ez fordított arányosságú humán műveltséget jelentene egyúttal), és ezt önigazolásképpen weöresi példával is alá lehet támasztani („nem megy a sinus-tétel, Sándor”). Még Karinthy is – aki matematika szakosként nyilván baráti viszonyban volt a számokkal – a hajdani matekórák jeges rémületének emlékével néz a fizikus-feltalálóra: „… a neve is trigonometria-órák lidércnyomását idézi. Cosynus. Cosinus alfa, plusz cosinus béta. Szembenlevő szög. Komoly dolog, nem lehet viccelni, vagy tudod, vagy nem tudod. Meg lehet bukni belőle.”

Pedig alig van olyan jelenség, érzés, állapot, emberi kapcsolat, amire ne találnánk egy jó geometriai vagy aritmetikai metaforát.

Micsoda költői erő van ezekben a fogalmakban: érintő, befogó, átfogó, többismeretlenes, egymást metsző, páratlan vagy helyi érték! József Attila fiatalkori versében (A számokról) minden ember egy 1-esnek felel meg, és hiába hatványozódik, oszt és szoroz, „ilyformán mindig 1 marad”. A matematikai műveletek megnevezésében rejlő művészi potenciált használja fel aztán az életbölcsesség megalkotásához: „Adódjatok össze, / Hogy roppant módon felnövekedvén, / Az Istent is, aki végtelenség, / Valahogyan megközelítsétek”.

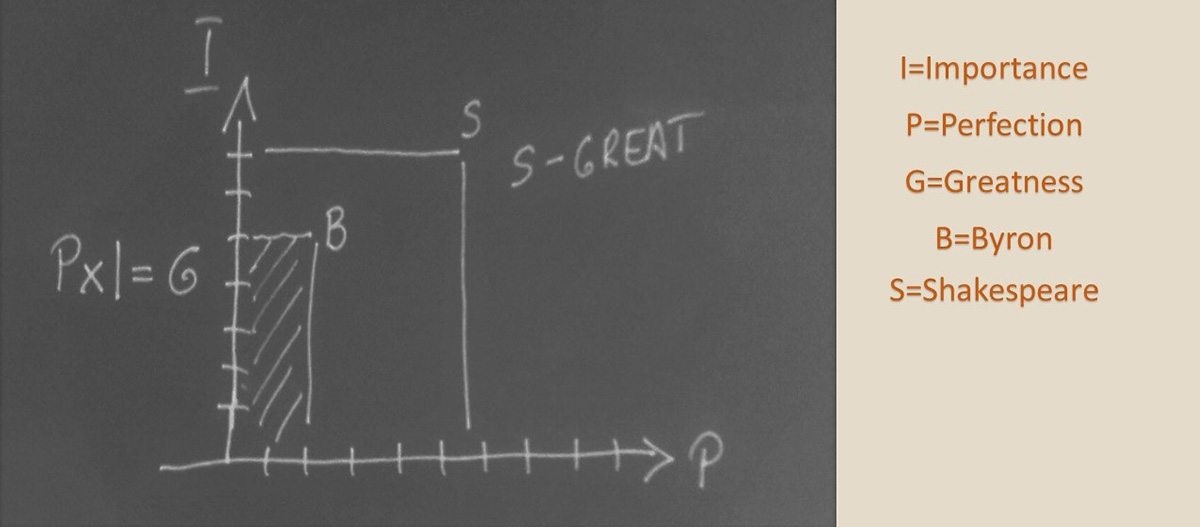
A Holt költők társasága egyik kulcsjelenetében Keating tanár úr – elrettentő példaként – a táblára rajzolja a lírai alkotásokhoz ajánlott megközelítési sémát. Noha nem vagyok kibékülve ezzel a filmalkotással, a ma tematikájához ez az ábra épp kapóra jön:

A vers értéke tehát úgy mérhető, ha a függőleges (y) tengelyen jelöljük, hogy mennyire fontos a cél, a vízszintesen (x-tengely) pedig, hogy ehhez a célhoz milyen szintű művészi kifejezésmód párosul: így kapjuk meg a vers nagyszerűségét jelző területet. „Excrement” – summázza véleményét a professzor, amellyel a nézőnek is azonosulni ildomos. De szentségtörés-e az irodalmat függvényen ábrázolni?

„A vers egy mindenütt folytonos, de seholsem differenciálható függvény. A vers változó irányú, egymást inverz transzformációsorozatokkal beburkoló erőterek kötöttfogású viaskodása egy telítetlen kontinuumban” – írja Szőcs Géza, aki természetesen szintén képekben beszél. Mindenesetre – ha van is bőven kivetnivaló a filmjelenet ábrázolta módszerben – az irodalom számokban való megközelítésével izgalmas dolgoknak jöhetünk a nyomára. Az irodalmi strukturalizmus már régóta tudja ezt. A stilometria statisztikai szövegvizsgálat segítségével jár utána, hogy miből adódik Ady vagy Krúdy sajátos nyelvi stílusa. A táblázatokban, gráfokban ábrázolt versek segítik az értő befogadást (és nem csak Weöres Sándor esetében).

Persze, nem minden szövegjelenségre találunk megfelelő mértékegységet: azt csak intuitíve tudjuk (de tudjuk!), hogy a poétikai intenzitás és a szavak számának hányadosa Pilinszky esetében minimum a harmincszorosa Zelk Zoltánénak. És az is világos, hogy a természettudomány törvényei nem mindig működnek irodalmi tartományban. Például ha Dante Isteni színjátékát a vízbe dobjuk, mindegy, mennyi vizet szorít ki, semennyit nem veszít a súlyából.

#nyelvműhely